世界座標
正方形タイルによる地図の表現で、地図が256×256の正方形タイルで表現されることが分かりました。
ズームレベル0では、以下のような1枚のタイルに世界地図が収まります。
※OpenStreetMapの地図画像を掲載しています。
このタイル上の位置を、左上の点を(0,0)、右下の点を(255,255)として、座標で表現したものを、Googleでは、世界座標と呼んでいるようです。
世界を、256×256で表現しているということは、赤道一周が256pixelで表現されていることになり、赤道上では1pixelあたり、約156kmということになります。当然、整数値では細かい位置が表現できませんので、実数で表現されます。
例えば、丹沢にある鍋割山荘の位置を世界座標で表すと、(226.9451598222222 , 101.01461503424304)と、ものすごく細かい数値になります。
ピクセル座標
画面上に地図を表示するには、ピクセル座標が必要になります。世界座標は、1枚の256×256の地図で表した場合の位置ですが、ズームレベルを上げた際には、全体のピクセル数は、512×512(ズームレベル1)、1024×1024(ズームレベル2)、…、16777216×16777216(ズームレベル16)、…のように増えて行きます。
その際の位置を表したのが、ピクセル座標です。
世界座標が決まれば、ピクセル座標は簡単に求めることができます。2^ズームレベル(２のズームレベル乗)を、世界座標に掛けるだけです。
ピクセル座標は、x、y、zで表されます。xは、左端からの順番、yは上端からの順番、zはズームレベルです。ズームレベル0の場合は、世界座標とピクセル座標は同じです。
先ほどの鍋割山荘の位置ですと、以下のようになります。ピクセル座標は、画像の1ピクセルに相当しますので、整数値としています。
| ズームレベルz | 倍率 | ピクセル座標x | ピクセル座標y |
|---|---|---|---|
| 0 | 2^0=1倍 | 226 | 101 |
| 1 | 2^1=2倍 | 453 | 202 |
| 2 | 2^2=4倍 | 907 | 404 |
| 3 | 2^3=8倍 | 1815 | 808 |
| … | … | … | … |
| 15 | 2^15=32768倍 | 7436538 | 3310046 |
| 16 | 2^16=65536倍 | 14873077 | 6620093 |
| 17 | 2^17=131072倍 | 29746155 | 13240187 |
つまり、鍋割山荘の位置は、ズームレベル0では、左から226ピクセル、上から101ピクセルの位置で、ズームレベル17では、左から29746155ピクセル、上から13240187ピクセルの位置ということになります。
このとき、x=29746155、y=13240187、z=17というピクセル座標が決まれば、地図上の位置が特定されることになります。
タイル座標
地図は、256×256ピクセルのタイル画像で用意されています。よって、特定の場所の地図を表示する場合は、このタイル画像をつなぎ合わせて表示することになります。
ピクセル座標x,y,zの3つの値が分かれば、タイルの座標も分かります。256ピクセルで1枚ですから、ピクセル座標を256で割った結果(整数値)がタイルの座標になります。
タイル座標が分かれば、その画像が取得できます。国土地理院の標準地図のタイルURLは、
URL：http://cyberjapandata.gsi.go.jp/xyz/std/{z}/{x}/{y}.png
となっています。
鍋割山荘を含む、ズームレベル(z) = 16の画像を取得したければ、
タイルX座標(x) = 14873077 / 256 = 58097
タイルY座標(y) = 6620093 / 256 = 25859
となり、
http://cyberjapandata.gsi.go.jp/xyz/std/16/58097/25859.png
の画像を取得すればよいことになります。
実際に取得してみると、以下の画像になります。
右が切れていて分かりづらいですが、1272三角点の右にある建物が、鍋割山荘です。
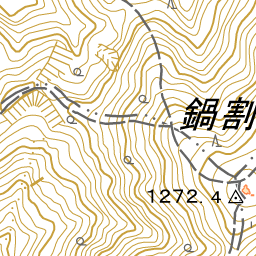※国土地理院提供の地形図を掲載しています。
また、このタイル内の鍋割山荘の位置は、256で割った余りとなります。
タイル内X座標 = 14873077 % 256 = 245
タイル内Y座標 = 6620093 % 256 = 189
左から245pixel、上から189pixelの位置が、鍋割山荘となります。
ちなみに、上の地図の右隣のタイルは、Xが+1されるので
http://cyberjapandata.gsi.go.jp/xyz/std/16/58098/25859.png
です。これを開いてみると、鍋割山荘の文字が見えると思います。
緯度、経度からピクセル座標への変換
世界座標が分かれば、ピクセル座標、タイル座標が計算できることが分かりました。ピクセル座標とタイル座標が分かれば、地図を表示することができます。
では、緯度、経度から世界座標を求めるには、どうすればよいでしょうか。
地図の表示でよく使われている、GoogleMaps API v3では、fromLatLngToPointというメソッドを呼べば、緯度・経度を世界座標に変換することができます。先ほどの、鍋割山荘の世界座標も、GoogleMapsで求めたものです。
しかし、TrailNoteでは、GoogleMapsを使っていませんので、独自に計算しなければいけません。それでは、どうやって緯度、経度を世界座標に変換するのでしょうか。
ネットで調べてみましたが、意外なほど情報が見つかりません。それでも、こちらのサイトに、計算方法が紹介されていました。世界座標を求めずに、直接緯度、経度をピクセル座標に変換する式ですが、アプリ内では、世界座標を使うことはなく、ピクセル座標ばかり使うので、こちらの方が都合がいいです。
以下のような式になるようです。
- 経度λとズームレベルzからピクセル座標xを計算する(式1)
- 緯度φとズームレベルzからピクセル座標yを計算する(式2)
※式2について、誤りのご指摘を受けまして、修正いたしました。
経度は、地球一周分がすべて含まれているため、単純に等分にするだけでよいということのようです。緯度は上限があることもあって、難しい式になっています。Googleマップ方式での表現可能な緯度の上限の正確な値は、このLの値となるようです。
この式で求めた結果が正しいかを、GoogleMaps APIの結果と比べてみます。
緯度、経度が変わっても問題ないことを確かめるため、利尻山（北海道）、雲取山（東京)、宮之浦岳（鹿児島）の山頂の座標で確認しました。
| 利尻山 | 雲取山 | 宮之浦岳 | |
|---|---|---|---|
| 山頂緯度 | 45.178506 | 35.855499 | 30.335927 |
| 山頂経度 | 141.242035 | 138.943905 | 130.504283 |
| 世界座標x GoogleMaps API |
228.43878044444443 | 226.80455466666666 | 220.8030456888889 |
| 世界座標y GoogleMaps API |
91.90981205708778 | 100.654443170873 | 105.34294822915888 |
| ピクセル座標x(z=17) GoogleMaps API |
29941927 | 29727726 | 28941096 |
| ピクセル座標y(z=17) GoogleMaps API |
12046802 | 13192979 | 13807510 |
| ピクセル座標x(z=17) 式1による計算 |
29941927 | 29727726 | 28941096 |
| ピクセル座標y(z=17) 式2による計算 |
12046802 | 13192979 | 13807510 |
GoogleMaps APIによる計算と、上記式での計算の、ズームレベル17でのピクセル座標が完全に一致しています。TrailNoteでは、ズームレベル17を越えるレベルは扱いませんから、このレベルで1ピクセルのずれも生じないのであれば、全く問題ありません。この式を使わせてもらうことにします。
これで、緯度、経度が分かれば、ピクセル座標、タイル座標が分かるようになりました。
ここまで分かれば、指定された座標を中心とした地図の表示ができます。
ピクセル座標から緯度・経度への変換
緯度・経度→ピクセル座標の変換式を使うと、地図の表示ができますが、地図をドラッグしたり、ルートの入力ができるようにするには、クリックされた位置の緯度・経度を知る必要があります。
そのためには、ピクセル座標→緯度・経度の変換が必要です。
こちらの計算も、先ほどのサイトの内容から引用させて頂きます。
以下の式となるようです。
- ピクセル座標x,zから、経度λを計算する(式3)
- ピクセル座標y,zから、緯度φを計算する(式4)
これは、経度・緯度からピクセル座標を求める式(式1、式2)の逆関数となっているため、先ほどの結果が正しければ、こちらも問題ないはずです。
先ほど求めたピクセル座標から緯度、経度を求めてみます。
| 利尻山 | 雲取山 | 宮之浦岳 | |
|---|---|---|---|
| 山頂緯度 | 45.178506 | 35.855499 | 30.335927 |
| 山頂経度 | 141.242035 | 138.943905 | 130.504283 |
| ピクセル座標x(z=17) | 29941927 | 29727726 | 28941096 |
| ピクセル座標y(z=17) | 12046802 | 13192979 | 13807510 |
| 式3による経度 | 141.242026 | 138.943899 | 130.504274 |
| 式4による緯度 | 45.178513 | 35.855501 | 30.335935 |
結果は、ほんの少し元の緯度、経度とずれていますが、これは、ピクセル座標を整数で丸めてしまったためです。ピクセル座標を実数で計算してから戻すと、同じ値になります。