旧バージョンでは、独自のアルゴリズムでトラックポイントを間引いていたのですが、とても処理が遅く性能も悪かったので、Ver1.2からは先人の知恵をお借りすることにしました。
調べた所、点を間引く方式としては、Douglas-Peuckerアルゴリズムが有名なようです。
Douglas−Peuckerアルゴリズム
Douglas-Peuckerアルゴリズムは、ラインを単純化するアルゴリズムで、とてもシンプルです。
手順は、以下のようになるようです(こちらを参考にしました)。
- ルートの始点、終点をプロット対象とする。
- プロット対象をつなげた直線と、その間の各点との距離を調べる。
- 許容距離(ε)以上離れた点で、最も離れた点を探し出し、そこを新たにプロット対象とする。
もし、ε以上離れた点がなければ、終了。 - 2〜3の処理を再帰的に繰り返す。
最も離れた点(ルートの形を特徴づける点)を残していき、近い点を削除していくことで、なるべく元の形を維持したまま点を間引くことができるということのようです。以下に実際の例を示します。
| 元の状態 | 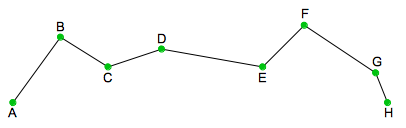 |
最初の状態が左のような点の集まりだとします。最初に「ε:許容距離」を決めます。 |
| ステップ1 | 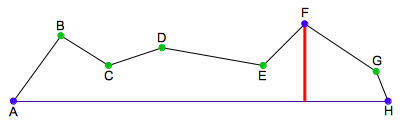 |
まず、開始点Aと終了点Hを結んだ直線AHと、途中の点B〜Gのすべての距離を調べ、一番遠い点を探します。 この場合、点Fが一番遠い点です。直線AHとFの距離が、εより大きいことを確認します。 この時点で点A、H、Fが確定します。 |
| ステップ2 | 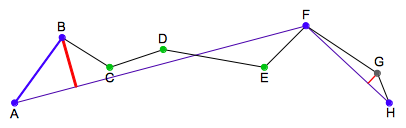 |
Fが確定したので、今度は、直線AFと直線FHについて、それぞれステップ1と同じ処理を繰り返します。ここでは、直線AFと一番離れた点Bとの距離がεより大きく、直線FHと点Gとの距離は、εより小さくなりました。 点Bが確定して、点Gは廃棄されます。 |
| ステップ3 | 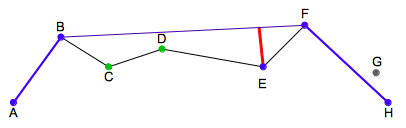 |
以下は同様に繰り返します。ここでは、直線BFと点Eの距離がεより大きいので、点Eが確定しました。 |
| ステップ4 | 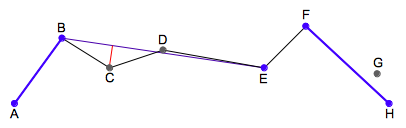 |
同様に、直線BEと、その間の点C、点Dの距離を調べますが、どちらもεよりも小さいことが分かりました。εより離れた点が見つからなくなったら終了です。 |
| 間引き終了 | 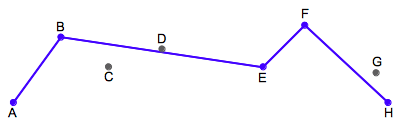 |
確定した点を繋げば、間引き後の線が残ります。 今回は、点C、点D、点Gが間引かれました。 |
この方法では、εの値を極端に大きくすれば、両端の点だけが残り、εを0にすれば、1つも間引かれなくなります。
点の数を指定して間引く
Douglas-Peuckerアルゴリズムは、許容距離ε以上離れた点だけを残すというものですが、このεの値にどのような値を指定すればよいのか、よく分かりません。GPSのログを間引くときは、点の数を5000個から1000個に間引くといったように、間引き後の点の数が指定できたほうが、使いやすいと思います。
そこで、Douglas-Peuckerアルゴリズムを少し変更して、以下のようにしてみました。
- ルートの始点と終点をプロット対象とし、確定リストに追加する。
- 始点と終点をつなげた直線から、最も離れた点を探し、その点を、距離やプロット開始点、終了点の情報と共に、プロット候補リストに追加する。
- プロット候補リストから、最も距離の遠い点について取り出し、その点を確定リストに入れる。
- その点より前の部分、後ろの部分を調べ、それぞれ最も離れた点を探し出し、その点を、距離やプロット開始点、終了点の情報と共に、プロット候補リストに追加する。
- 3〜4を繰り返す。
- 確定リストの点の数が目標数に到達したら、終了。
このように、最も距離が遠い点から確定させていき、指定した数の点数になるまで続けることで、点数の指定ができるようにしています。
上記の例で、間引き後の点数を6とした場合は、以下の表のようになります。
| ステップ | プロット候補リスト | 確定リスト |
|---|---|---|
| ステップ1 | F | A, H |
| ステップ2 | B, G | A, F, H |
| ステップ3 | E, G | A, B, F, H |
| ステップ4 | C, G | A, B, E, F, H |
| ステップ5 | G, D | A, B, C, E, F, H |
間引き後の点数が5の場合は、ステップ4で終わります。そのとき、Douglas-Peuckerアルゴリズムの説明で使った例と同じ結果になっています。
プロット候補リストの中は、距離の遠い順で、点が並びます。
この方法では、どんなに近い点でも候補リストに入ります。そのため、Douglas-Peuckerアルゴリズムでは、真っ先に廃棄された点Gも候補リストに入っています。しかし、点Gは距離が近いため、後から追加された点EやCよりも後回しにされます。
この例では、点が少ないのでプロット候補リストが小さいですが、実際は沢山の点が候補リストに並ぶことになります。
このDouglas-Peuckerアルゴリズムを応用した方式に変更してから、旧バージョンの独自アルゴリズムと比べて、格段に速くなりました。1万個のトラックポイントも、瞬時に、間引くことができます。
問題点と改善策
Douglas-Peuckerアルゴリズムは、とても性能がよく、かつ高速で良さそうですが、GPSのログを間引く際に、そのまま適用すると少し問題があります。
- 山頂のポイントが、間引かれてしまうことがある
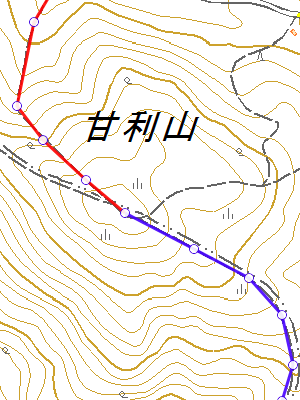
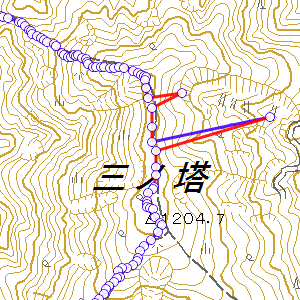
以下のように、山頂で進行方向が変わらない場合、山頂のポイントが間引かれてしまうことがあります。
 |
 |
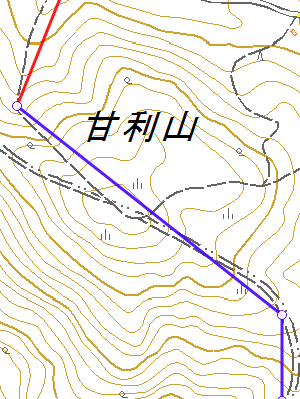 |
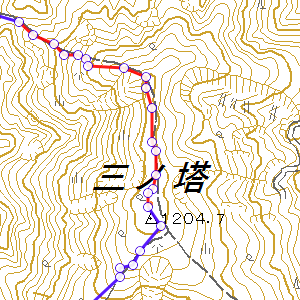
| 元のトラックポイント | 間引き後のトラックポイント |
※国土地理院提供の地形図を掲載しています
これは、山頂で直進しているため、山頂の点を間引いてもルートの形が維持できると判断されているためです。しかし、山頂の点が間引かれると、累積標高などが大きく変わってしまいます。
幸い、TrailNoteでは常にルート上のピークとコルを検出しています。その情報を使い、ピークやコルの点であれば、ものすごく遠い点として計算するようにしました。そうすると、ピークやコルは最も残すべき点として認識されますので、優先的に残されます。
- 休憩中のポイントが沢山残ってしまう
GPSのログは、機器の性能で大きく変わってしまいます。例えば、山小屋に宿泊したような場合で、夜間ずっとGPSのログを取りつづけたときに、以下のように動きまわる点が取得されることがあります。
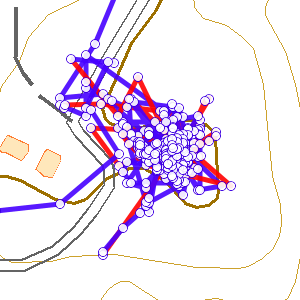 |
 |
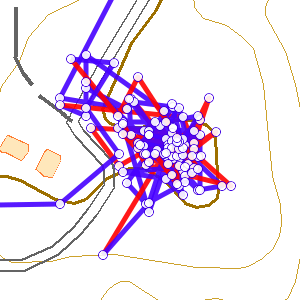 |
| 元のトラックポイント | 75%間引いた後のトラックポイント |
この例では、夜中に900ポイント以上のログをとっており、3km以上も行動したことになってしまっています。
このような細かく動くログを、Douglas-Peuckerアルゴリズムで間引くと、右の結果のように、沢山の点が残ってしまいます。これは、点が向きを変えて動くと、それを優先して残してしまうためです。
そこで、間引きをする前に休憩箇所を調べることにしました。2分以上、動きがほとんどない箇所を探し、それを休憩と判断しています。
休憩開始・終了の点は、上記のピークとコルと同様、残すようにし、休憩中の点は、距離を小さくすることで、積極的に消すようにしています。この条件を追加したところ、休憩中のポイントが優先的に間引かれるようになりました。
休憩中の点を間引くことで、GPSの誤差による行動距離も削られるので、より正確な距離になると思います。
- GPSログの暴れを間引く
GPS機器の性能は、年々向上しているようですが、場所などの条件によっては、時々、トラックポイントが、遠くに飛んでしまうようなことがあるようです。
そのような1つだけ遠くに飛んでしまった点を、Douglas-Peuckerアルゴリズムで間引いた場合、その点は、特徴的な点として把握されてしまい、確実に残されてしまいます。
そのような点は、間引きをする前処理で除去するようにしてみました。今のところ、以下のような簡単なルールで取り除いています。
・前の点との距離、時間差から速度を計算すると、時速10km以上出ている。
・その点を取り除いて、その前後の点の速度を計算すると、時速5km以下になる。
 |
 |
 |
| 元のトラックポイント | 間引いた後のトラックポイント |
上の例のように、飛んでしまっているポイントが取り除かれます。
時速10kmの条件では、走った場合に困りそうですが、2番目の条件によって除外されます。
このような異常なポイントだけ削除したい場合は、間引き後の点数を元の点数に近い値(例えば、1000ポイント→990ポイント)にして、間引きを行えば最優先で除去されます。
上記のように色々と工夫はしてみていますが、間引きの方法は奥が深いようで、まだまだ改善の余地があると思います。何か良い案などありましたら、教えていただきたいと思います。

